High-frequency (HF) tags and readers use inductive coupling to communicate. Ultrahigh-frequency (UHF) tags can also employ inductive coupling in the near field. Why can’t 2.4 GHz inductive coupling be utilized?
—Name withheld
———
That’s an interesting question, and the answer is beyond my knowledge of RF engineering, so I reached out to Neeraj Sood, a researcher at the University of Toronto and a member of McMaster University‘s RFID Applications Lab. Here is an edited version of Neeraj’s response:
“I assume that we are talking about a passive system using inductive coupling, and not an active system. Inductive coupling works in the near field of the reader antenna. The electrical current flowing through the reader antenna produces a magnetic field. When the tag’s antenna is placed in this magnetic field, it produces a current in the tag antenna that allows tag-reader communication to take place.
“The strength of the magnetic field is proportional to 1/r^3, where r is the radial distance from the reader antenna. This means that as we increase the radial distance from the near-field reader antenna, the field’s strength decays as the cube of this distance—a very rapid rate of decay [see the graph below]. Therefore, to use inductive coupling, the tag should be placed less than 0.16 wavelengths away from the reader.
“For passive HF RFID systems, the wavelength is around 22 meters [72 feet], which allows for the tag to be placed a reasonable distance from the reader antenna. However, at 2.4 GHz, the wavelength is quite small—around 12.5 centimeters [4.9 inches]. That means the tag would need to be placed less that 2 centimeters [0.8 inch] from the reader antenna, which would not be useful for most data-collection needs.”
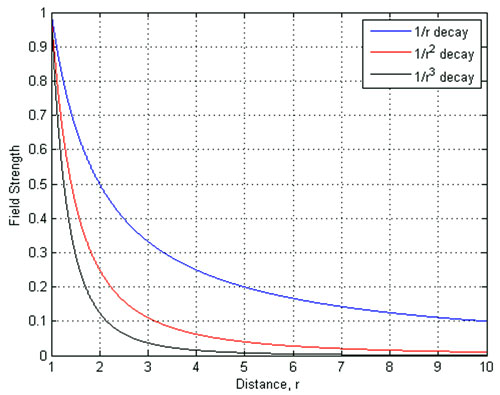
To view a larger version of this graph, click here.
—Mark Roberti, Founder and Editor, RFID Journal

